Почему отказался от премии 1 миллион зелёных и стал затворником великий русский математик Перельман

Некоторые источники об ошибочно утверждают, что отец Григория Перельмана, Яков Исидорович Перельман, был известным физиком, астрономом и математиком, однако это не соответствует действительности. На самом деле, они просто однофамильцы, не имеющие родственных связей.

О гипотезе Пуанкаре. Лекция в Яндексе

Гипотеза Пуанкаре, озвученная французским математиком Анри Пуанкаре в 1904 году, имеет свои корни еще в XIX веке. В то время было установлено, что если любую замкнутую петлю на двумерной поверхности можно сжать до одной точки, то данную поверхность можно превратить в сферу. Например, поверхность воздушного шарика действительно поддается такой трансформации, тогда как поверхность бублика — нет. Это связано с тем, что в случае бублика, как мы можем легко представить, петля не может быть стянута в точку. Данная гипотеза утверждает, что аналогичное утверждение справедливо для трехмерных многообразий.

Только в 2003 году гипотезу Пуанкаре удалось доказать, и это достижение принадлежит нашему соотечественнику Григорию Перельману. В этой лекции рассматриваются объекты, необходимые для формулировки гипотезы, история поиска ее доказательства и ключевые идеи, стоящие за ним.

Лекцию читают доценты механико-математического факультета МГУ кандидат физико-математических наук Александр Жеглов и кандидат физико-математических наук Федор Попеленский.

Если не углубляться в математические детали, ее смысл можно формулировать следующим образом: как можно охарактеризовать (трехмерную) сферу? Чтобы разобраться с этим вопросом, необходимо понять одно из ключевых понятий в топологии — гомеоморфизм. Осознав, что это такое, мы сможем четко сформулировать гипотезу Пуанкаре.

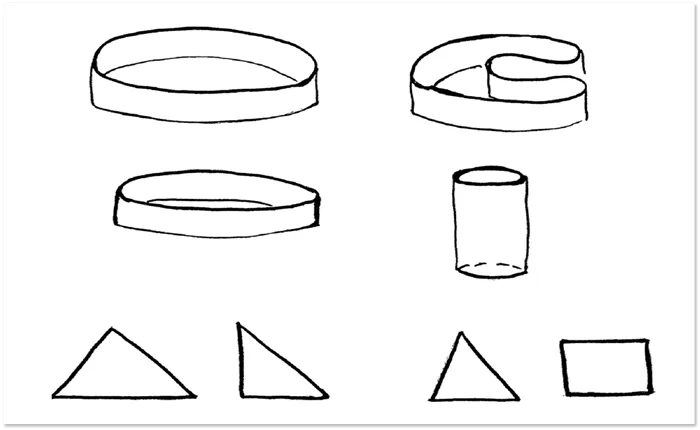
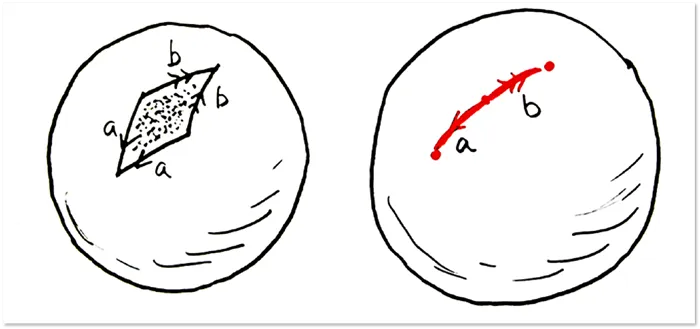
Чтобы избежать чрезмерного погружения в математические формулировки, скажем просто, что две фигуры считаются гомеоморфными, если имеется возможность установить между их точками взаимно однозначное соответствие, при котором близким точкам одной фигуры отвечают близкие точки другой фигуры и наоборот. Пропущенные детали касаются правильного определения понятия близости точек.

Понимание того, что две фигуры являются гомеоморфными, становится очевидным, если одну фигуру можно получить из другой с помощью произвольной деформации, где не допускаются изменения поверхности, такие как разрывы, сворачивание областей в точку или создание дырок.

Более точное, хотя все еще не окончательное, понимание гомеоморфных фигур может быть достигнуто, если разрешить возможность разрезать фигуру, перекручивать и завязывать, затем заклеивать разрез как было. Это позволит учесть большее количество возможных преобразований поверхности.

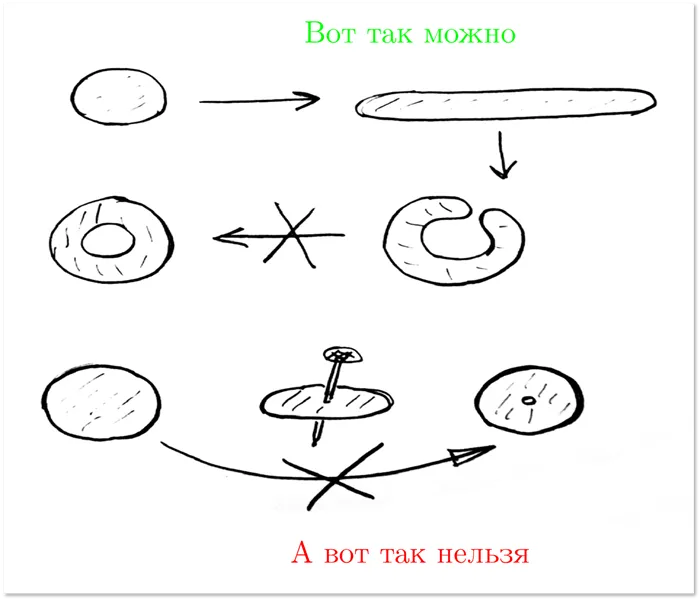
Рассмотрим еще один пример. Представим себе яблоко, в котором червяк сделал ход, напоминающий узел, и небольшую пещеру.

С точки зрения топологии поверхность данного яблока все еще будет оставаться сферой. Это можно объяснить тем, что, если правильно провести деформацию, то мы можем вернуть яблоко к его первоначальному виду, несмотря на то, что в нем появилась пещера от червяка.

Для закрепления пройдитесь по классификации букв латинского алфавита с точки зрения гомеоморфизма (т.е. выясните, какие буквы являются гомеоморфными, а какие — нет). Результат зависит от начертания букв (например, шрифта или гарнитуры), и для простейших начертаний он будет представлен на следующем рисунке:

Формальная постановка вопроса

Пусть M — замкнутое связное многообразие размерности 3, и пусть на нем любая петля может быть стянута в точку. Следовательно, M гомеоморфно трехмерной сфере.

Наибольшую трудность для неподготовленного человека на данном этапе представляет понятие многообразия размерности 3, а также характеристики, описываемые словами «замкнутое» и «связанное». Поэтому целесообразно разобраться с этими понятием на примере двумерного размерности: в этом случае многое становится значительно более простым.

Управлять Вселенной по Перельману. В чем суть теоремы Пуанкаре?

29 сентября 2016 года, 08:37:38 — В истории науки не так много людей, которые оставили заметный след. Нам повезло, что в одно время и в одной стране жил математический гений, который смог разгадать одну из загадок тысячелетия — Григорий Перельман. Но что такое теорема Пуанкаре и какое значение она имеет для изучения Вселенной?

Будущий ученый родился в Ленинграде в интеллигентной семье. Перельман закончил школу с отличием, но не получил золотую медаль, так как не сдал нормы ГТО. Тем не менее, он был зачислен на механико-математический факультет Ленинградского государственного университета без экзаменов. Позже он поступил в аспирантуру при Математическом институте имени В.А. Стеклова, где защитил кандидатскую диссертацию и остался работать.

Трудные 1990-е заставили молодого исследователя переехать в США. Там он обратил внимание на одну из самых сложных, на тот момент еще не решенных, задач современной математики — теорему Пуанкаре. Позже Перельман отметил, что подсказку для доказательства этой теоремы дал ему американский математик Ричард Гамильтон, который на своей лекции рассказывал о потоках Риччи — новом инструменте, используемом для исследования гипотезы геометризации Тёрстона, которая является обобщением гипотезы Пуанкаре. Объяснить простым языком суть гипотезы сложно, но все же стоит попытаться. Представим себе сферу, все точки которой равномерно удалены от центра. Перед нами двумерное тело, но гипотеза касается трехмерного тела. Все точки трехмерного тела также будут находиться на одинаковом расстоянии от центра. Проблема заключается в том, что в отличие от двумерных сфер, трехмерные объекты невозможно увидеть наглядно, что затрудняет наше представление о них. Именно для этого и существует теоретическая математика.

Теорема Пуанкаре рассматривает именно такие метаморфозы трехмерных тел в многомерном пространстве. Если представить шар и тор (форму пончика), то одну фигуру нельзя получить из другой без разрыва: тела такой формы неизбежно разрушатся. Однако конус, куб или цилиндр могут быть легко трансформированы из одного в другое. Трехмерные шар и тор являются компактными и односвязными сферами, т.е. их можно сворачивать и разворачивать в одну точку. Анри Пуанкаре утверждал, что Вселенная на самом деле представляет собой такую трехмерную сферу, что можно свернуть или развить в точку и обратно. Доказательство истинности этого утверждения заняло почти сто лет.

Вернувшись на родину, Григорий Яковлевич практически не покидал свой дом. На поиск решения этой сложнейшей задачи у него ушли недели, однако результат стоил всех тех усилий и самоотречения. В 2002-2003 годах Перельман опубликовал в Интернете три своих знаменитых статьи, кратко излагающих метод доказательства гипотезы. Ученый смог нейтрализовать образование сингулярных (неопределенных) зон с использованием потоков Риччи, и многообразие успешно преобразовалось в сферу. Многие ученые, в особенности сотрудники Массачусетского технологического института (MIT), скептически отнеслись к открытию Перельмана, утверждая, что он использовал неподходящий метод для решения этой задачи. В то время никто не подозревал, что потоки Риччи, представляющие собой определенное уравнение в частных производных, похожее на уравнение теплопроводности, можно применять для решения гипотезы Тёрстона.

В одной из своих статей Перельман утверждал, что теорема Пуанкаре помогает в исследовании сложных физических процессов в рамках теории мироздания и дает ответ на вопросы о форме Вселенной. Доказательство теоремы Пуанкаре имеет огромное значение для развития нанотехнологий, поскольку оно позволяет сжимать объекты до одной точки и восстанавливать их обратно. Теоретически такой эксперимент можно провести и над всей Вселенной. Однако пока ни один ученый не может точно предсказать, что произойдет с человечеством в результате этого.

Экспертиза

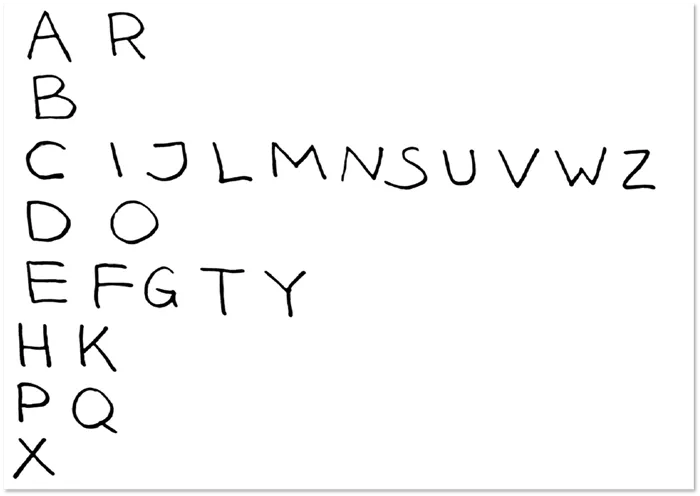
Фрау Лора Смит
Преподаватель английского языка

Dficia deserunt mollitia animi, id est laborum eu
Nam libero tempore, cum soluta nobis est elieni
omnis voluptas assumenda est, omnis dolo
resed repellendus temporibautem.

Если вы хотите поделиться своими научными исследованиями, разработками и открытиями, пишите нам по следующему адресу: sciencemedialab@yandex.ru

Почему Перельман отказался от премии в 1 миллион долларов и стал затворником, величайший русский математик

Получайте на почту один раз в сутки одну самую читаемую статью. Присоединяйтесь к нам на Facebook и ВКонтакте.

Имя Григория Перельмана, величайшего математика нашего времени, стало известно миру около полтора десятка лет назад. Он смог разрешить загадку, которая оставалась неразгаданной более столетия — доказал гипотезу Пуанкаре. Это одна из самых сложных математических задач в истории науки. Позже Перельман шокировал общество своим отказом получатьсамую престижную награду в области математики — медаль Филдса и денежную премию в один миллион долларов! Почему же великий ученый поступил таким образом и выбрал затворническую жизнь, предпочтя существование полной изоляции? Давайте разберемся далее.

Рождение и становление гения

Григорий Яковлевич Перельман появился на свет 13 июня 1966 года в Ленинграде (сейчас Санкт-Петербург). Его семья имела еврейские корни. Отец Григория не имел никакого отношения к науке — был обычным инженером. Его часто путают с однофамильцем — физиком и математиком Яковом Перельманом. Некоторые невнимательные исследователи даже сочли это родство не случайным, потому что так объясняли бы страсть Григория к математике. Однако, этот факт интересен и в какой-то степени неожиданный: к математике любовь привила будущему гению мать, Любовь Лейбовна Перельман, которая была преподавателем математики в советские времена. Кроме этого, она увлекалась музыкой и училась играть на скрипке; преподаватели отмечали ее таланты.

Эта любовь к математике и музыке послужила источником вдохновения для его дальнейшего выбора жизни. В тот момент, когда он стоял перед выбором своей пути, его манили как консерватория, так и технический университет. После долгих раздумий он все же выбрал последний.

В школе Григорий отлично учился. Он проявлял способности не только к математике, его речь была логичной и грамотной на таком уровне, что учителя просто поражались. В старших классах его способности были замечены, и он был переведен в физико-математическую школу, что значительно способствовало развитию его научного дарования. Во время учебы в школе Перельман несколько раз становился победителем математических олимпиад. Главным достижением стала золотая медаль на Международной математической олимпиаде в 1982 году, проходившей в Будапеште.

После трудного выбора между карьерой музыканта и ученого, Григорий все-таки поступил в Ленинградский государственный университет (ЛГУ) и был зачислен на механико-математический факультет без экзаменов. Это не помешало ему, несмотря на отсутствие золотой медали, получить настоящую научную карьеру, поскольку мы видим это как результат блестящих успехов в науке и учебе. Единственный фактор, который помешал ему получить медаль, так это низкая оценка по физкультуре.

После успешного окончания университета Григорий Перельман поступил в аспирантуру, защитил кандидатскую диссертацию и стал старшим научным сотрудником. Вскоре он получил приглашение переехать и работать в США. Он принял это предложение и несколько лет жил и работал в Соединенных Штатах. В отличие от многих талантливых молодых людей, американская мечта его не привлекла, и он вернулся на родину, где Пуанкаре не оставил его в покое — идею разгадать головоломку о гипотезе все еще преследовала его.

Личная жизнь

Масштабный поворот в жизни ученого вызвал большой интерес у его коллег, журналистов и обычных граждан. Наибольшее количество вопросов возникло после того, как Перельман отказался получать присуждённую ему медаль Филдса, которая является аналогом Нобелевской премии в математике, и премию тысячелетия в размере одного миллиона долларов, присуждаемую институтом Клэя за решение одной из семи загадок мира. Гипотезу Пуанкаре также включили в этот список.

Когда мировое научное сообщество узнало об открытии Григория Перельмана, учредители премий связались с ним. Однако, к всеобщему удивлению, он отказался от этих денег и даже не объяснил причин своего решения.

Спустя некоторое время Григорий полностью закрылся от журналистов. Отечественные журналисты не могли получить от него ни комментариев, ни ответов, а зарубежным он отвечал, но интервью не давал. Его поведение стало источником множества слухов и сплетен, появились утверждения о том, что он серьезно болен и что ему поставили неутешительный диагноз — аутизм. Тем не менее, ни одного медицинского заключения в подтверждение этого не было обнародовано, и утверждать, что это правда, не представляется разумным.

Григорий Перельман сегодня

В настоящее время ученый живет с тяжело больной матерью, сам же не создал свою личную жизнь — у него нет ни жены, ни детей. Единственным человеком, с кем он поддерживает связь, является его школьная учительница. Она сообщила, что Перельманы живут очень скромно, если не сказать бедно.

В 2018 году появились слухи о том, что Григорий переехал на постоянное место жительства в Швецию. Однако эту информацию вскоре опровергли соседи ученого и продавцы ближайших магазинов, в которые Григорий ходит за покупками. Выдающийся ученый продолжает вести затворнический образ жизни в своей квартире на окраине города на Неве.

Что доказал Григорий Перельман, если говорить простыми словами

Григорий Перельман доказал, что все трехмерные многообразия определенного вида могут быть сведены к трехмерной сфере.

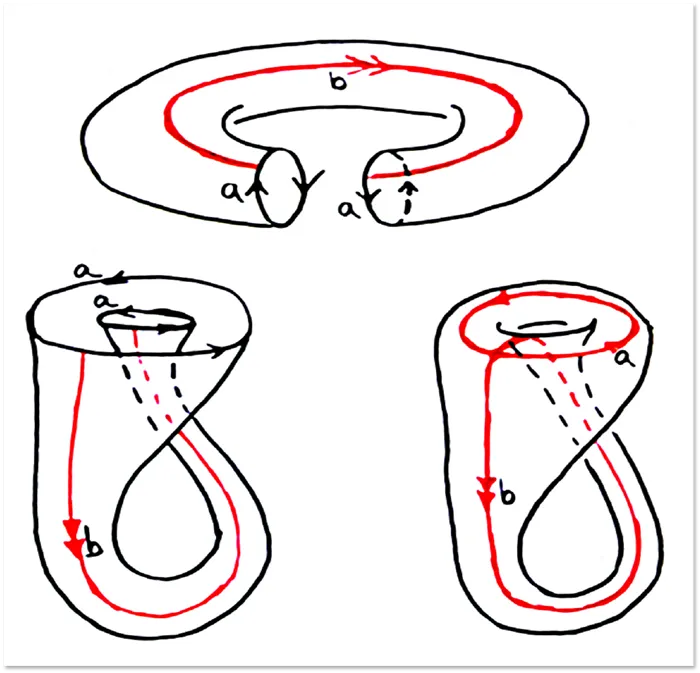
Чтобы лучше понять, представьте себе двумерные многообразия, такие как сфера, тор или поверхность цилиндра. Поверхность цилиндра можно трансформировать в сферу, если провести нужные деформации, такие как растягивание или изгиб. Это означает, что поверхность цилиндра гомеоморфна сфере. Однако, ни при каких обстоятельствах невозможно превратить тор в сферу: дыра в торе никуда не исчезнет, каким бы образом вы не пытались его изменить. Однако простая кружка может быть легко преобразована в тор, следовательно, она гомеоморфна тору:

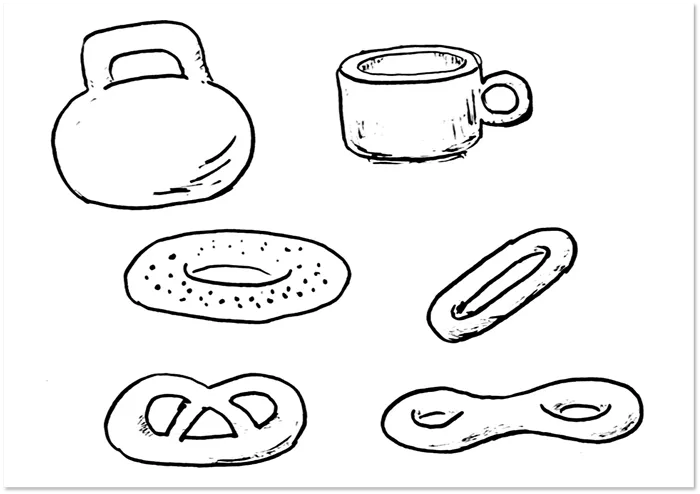
Таким образом, Пуанкаре сформулировал свою гипотезу для трехмерных многообразий, утверждая, что определенный класс таких многообразий можно свести к трехмерной сфере аналогично тому, как тор сводится к кружке и поверхность цилиндра к сфере. И это доказал Перельман.

Визуализировать все это может быть сложно и не всегда необходимо. Однако, если вам интересно лучше понять суть вопроса, рекомендуется читать книгу британского математика Иэна Стюарта Величайшие математические задачи, где также освещается тема Перельмана.

“Вселенная заточена под меня…” отрывок из фантастической серии “Контролёр” Юрия Никитина

Всякое односвязное компактное трехмерное многообразие без края является гомеоморфным трехмерной сфере.

После доказательства этой гипотезы, авторство которой принадлежит Григорию Перельману, правильнее использовать название теорема Пуанкаре-Перельмана.

Теперь с высокой вероятностью можно утверждать, что наша Вселенная действительно является той самой трехмерной сферой. Она не имеет края, что и обосновывает идею бесконечности. Топология сообщает нам, что такая сфера легко сжимается в точку и совершенно так же разворачивается из нее. Это поддерживает теорию большого взрыва: сейчас мы находимся в процессе расширения, но со временем можем снова начать сжиматься. В этой связи уместно вспомнить библейское выражение: «время собирать камни и время разбрасывать камни».

Возникает вопрос: что заставляет Вселенную сжиматься и разжиматься? Ответ на этот вопрос может дать работа Станислава Лема и Юрия Антомонова. Можно предположить, что единственная цель и смысл существования материи — самопознание. В определенный момент развития материи (используя для этого человека) она может становиться разумной, и, достигнув универсальности и самодостаточности, не зависеть от материальных форм (чистый разум или Дух). Вселенная в этот момент будет напоминать океан Солярис, состоящий из информационного поля, которое сможет создавать любой материальный объект, как описывал это Лем. В конце концов, когда материя познает саму себя в полной мере, ее миссия завершится, и она просто перестанет существовать.

Скорее всего, этот процесс будет длиться так же долго, как и предыдущее расширение. Есть соблазнительное предположение, что на этом этапе время может потечь вспять, чтобы поддержать гармонию и целостность картины. Например, когда мы пересматриваем видео в обратном порядке, таймер в углу экрана начинает идти обратно. И именно эта пульсация: из ничто в все и из всего в ничто — и есть сущность бытия Вселенной.

С чем это отличается от религиозного взгляда на мир, так это в том, что в религии Вселенский Дух, то есть Бог, изначально мудр и не нуждается в самопознании. Он просто развлекается с материей и людьми, чтобы избежать скуки, и не совсем понятно, откуда появился такой продвинутый Дух.

Вот и вкратце все основные мысли.