Чертежи без линейки и еще 3 способа разобраться с геометрией

Допустим, вам поручено выбрать и купить новую плитку для ванной комнаты. Как это часто бывает, у вас есть строгий бюджет, и превышение суммы в 3000 рублей не допускается. В одном из магазинов вы находите плитку, которая подходит по цвету и ценой составляет 600 рублей за 400 квадратных метров.

Какова роль геометрии? И что такое геометрия?

Геометрия — это одна из важных областей математики, которая изучает свойства фигуры и пространственные отношения. Зачем она вообще нужна? Каждый раз, когда мы сталкиваемся с новым предметом, у нас появляется много вопросов. И давайте откроем один из древних мифов. Входя в академию Платона, каждый мог увидеть надпись, которую сам filósofo вырезал на камне:

Пусть сюда не входит тот, кто не знает геометрии.

И вы знаете, с Платоном трудно не согласиться. Возникает естественный вопрос о важности геометрии. Всё вокруг нас окружает нас предметами, обладающими формой, объемом, площадью и периметром. Будь то компьютерная мышь или коробка из-под обуви.

Это правда: наш мир состоит из предметов. Геометрия — это наука о свойствах этих предметов и их взаимосвязях. Чтобы лучше понять этот предметный мир, в котором мы обитаем, невозможно обойтись без геометрических знаний.

Поэтому мы приглашаем вас в удивительное путешествие по познанию окружающего мира. Предлагаем вам нечто вроде входного билета в академию Платона и возможность получить основательные знания о пространстве и формах вокруг нас.

Итак, что изучает геометрия?

Геометрия — это раздел математики, который исследует пространственные формы и принципы их измерения.

Рассмотрим тот же пример: вас попросили купить новую плитку для ванной комнаты. Однако у вас вновь ограниченный бюджет, который нельзя превышать 3000 рублей. Вы нашли плитку, подходящую по цвету и цене — 600 рублей за 400 квадратных метров.

Что делать? Какой объем плитки вам следует купить? Или нужно искать более выгодные предложения?

Вот вам и ответ на вопрос, зачем нужна геометрия. Во-первых, знания геометрии помогут вам определить площадь пола в ванной. Соответствующими инструментами вы измеряете длину и ширину пола в метрах. Умножив их, вы получите площадь, измеряемую в квадратных метрах.

Во-вторых, используя математические навыки, вы сможете рассчитать, сколько плиток войдет в указанную площадь пола. Учитывая аспекты геометрии, за несколько минут вы сможете ответить на все три вышеуказанных вопроса.

Продуктивное сотрудничество!

Мы надеемся, что вы это чувствуете. Геометрия анализирует фигуры, а математика помогает количественно выразить их. Они всегда действуют в тандеме.

Что изучает геометрия: геометрические фигуры на практике

Фактически, любой предмет, который вы видите сейчас, можно разложить на элементарные геометрические фигуры. Обратите внимание на ваше окружение: экран компьютера или смартфона представляет собой прямоугольник. Бутылка с лимонадом имеет форму цилиндра. Контуры автомобиля можно сравнить с трапецией. Высокая электромачта выглядит как треугольник. Наручные часы представляют собой круг. И так далее.

Ле Корбюзье, великий французский архитектор, однажды писал: «Всё вокруг — это геометрия». Поэтому, возможно, с лёгким налётом древнегреческой иронии можно заметить: что же изучает геометрия? Она изучает всё!

Кстати, этим рисункам более пятнадцати тысяч лет. Судя по композиции, древние художники имели довольно глубокое понимание пространства и геометрических форм. Что тут скажешь, геометрия поистине изначальна и естественна. Благодарим греков за то, что они формально её описали.

Границы геометрии безграничны — от изучения свойств простого треугольника до исследовательских работ над экстремальными черными дырами и многомерными пространствами. Школьный курс ограничения в основном сосредоточен на планиметрии, которую изучают с 7 по 9 класс, и стереометрии, вводимой в старшей школе.

Планиметрия

Планиметрия — раздел геометрии, который исследует фигуры, находящиеся в двухмерном пространстве.

Представьте, что пол является плоскостью, и вы смотрите на предметы сверху. В этом случае объем их не учитывается. Основными концепциями планиметрии являются прямая линия и точка — из этих элементов составляются все фигуры. Например, треугольник.

Стереометрия

Стереометрия — это раздел геометрии, который исследует фигуры, находящиеся в трехмерном пространстве.

Наша реальность не ограничивается две измерениями — она имеет третье измерение. Поэтому стереометрия ближе к реальности, так как учитывает объем. Тем не менее, как видно, фигуры стереометрии могут быть представлены также в планиметрических формулах и концепциях.

С какого возраста начинается изучение геометрии в школе? Зачем это нужно?

До 7 класса ученики изучают обширные вопросы математики, и на этом этапе в 7 классе программа разделяется на две самостоятельные дисциплины – алгебру и геометрию.

У многих школьников геометрия вызывает ассоциации с бессмысленными формулами и расчетами, которые, по их мнению, в жизни абсолютно не нужны. Однако основная цель этой дисциплины вовсе не в том, чтобы заставлять детей страдать и разрушать их успеваемость.

Безусловно, геометрия полезна архитекторам, строителям, конструкторам. Это также поможет и при выполнении мелкого ремонта в квартире. Но задаться вопросом: разве мы каждый день занимаемся ремонтом или поклейкой обоев? Вероятнее всего, нет. Так зачем тогда тратить годы на изучение этого предмета? Поясняем.

Этот раздел наук развивает логику у детей. Возможно, в 99% случаев вы не будете использовать все сложные теоремы в повседневной жизни, но решение геометрических задач положительно влияет на работу мозга и развивается гибкость мышления в нестандартных ситуациях.

Почему детям сложно понимать геометрию?

Причины

• Неинтересность преподавателя или репетитора в объяснении teории детям

Ученики приходят в 7 класс после летних каникул, находясь в разгаре переходного возраста. Им охота веселиться, гулять с друзьями, а в школе от них требуют заучивания непонятных фраз и решение сложных задач. Преподаватели обязаны вовлекать детей в изучение геометрии и проводить параллели с реальной жизнью. Объяснять задание можно даже в простой и доступной форме, лишь бы это удерживало внимание школьников.

Учащиеся иногда прямо спрашивают у своих учителей о важности изучаемого предмета. Обычно диалог звучит так:

— Зачем нам каждый год проходить курс геометрии?
— Нуу… это просто часть образовательной программы, — отвечают учителя и репетиторы.

• Дети сознательно не хотят углубляться в предмет

Им не объяснили суть изучения данного раздела математики, поэтому у них возникло отторжение и нежелание понимать основы. Неведение накапливается, как снежный ком, и без базовых знаний дети не могут решить даже простые задачи.

Не все учебные пособия подают информацию доступно. Некоторые книги могут навалить материала на ученика, неразборчиво и неструктурированно.

А можно ли понять геометрию, если ученик на уроке боится задать вопрос? Некоторые невоспитанные учителя позволяют себе высмеивать учеников, что может вызвать чувство стыда. Это ужасная ситуация, и, к сожалению, такие вещи происходят.

Настоящий педагог должен быть другом для своего ученика. Отношения между учителями и детьми должны выстраиваться в дружелюбной и спокойной обстановке.

Как сэкономить на поступлении ребенка в университет?

Подпишитесь на нашу рассылку, и мы отправим вам детальную информацию о льготах на обучение и возможностях поступления на бюджетные места в престижные вузы без экстерната.

Всё рисуйте вручную

Это первое правило, которое нам объяснили на уроках в математической школе. Рисуйте все рисунки к задачам сами, без использования линейки. Если вы не удалось нарисовать с первого раза, рисуйте снова и снова. Чем больше вы рисуете, тем лучше осознаете все аспекты задачи.

Рекомендуем вам обращать внимание на учебник Р. К. Гордина «Планиметрия. 7–9 классы» — он действительно может помочь школьнику улучшить понимание геометрии, даже если на школьных уроках его это вокруг отбивает интерес.

Какой из советов вам наиболее интересен? Делитесь своими мыслями в комментариях!

Вы находитесь в разделе Блогов. Мнение автора может не соответствовать позиции редакции.

Фото: British Library / Wikimedia Commons / Public domain

Записывайте доказательства в два столбца

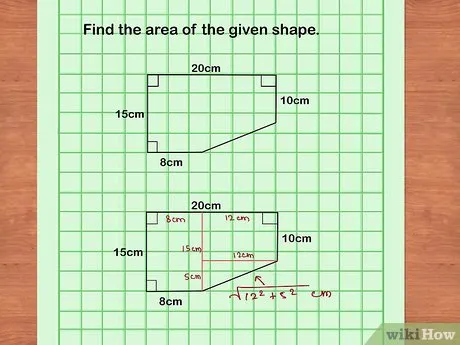
• Ясно обозначьте на рисунке все данные, представленные в задаче, и то, что нужно найти.
• Чем яснее будет ваш рисунок, тем легче вам удастся разрешить задачу.

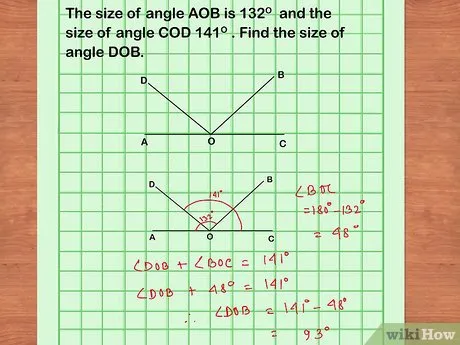
• Запишите отношения между длинами различных отрезков и сторон, которые можно выявить из вашего рисунка и предположений.
• Запишите все данные, указанные в задаче. Условия любой задачи по геометрии содержат исходники. Важно записать их таким образом, чтобы они были всегда под рукой во время решения.

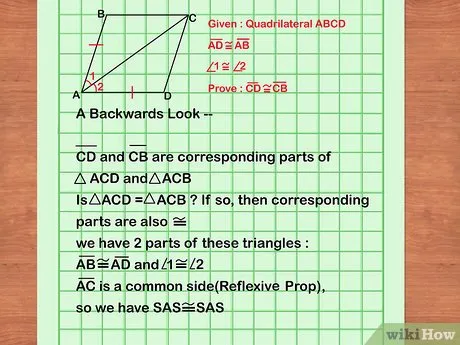
• Подумайте, как исходные данные могут привести к конечному результату.
• Существует ли логика и очевидные предположения, доказательства которых позволяют достичь заключительного результата?

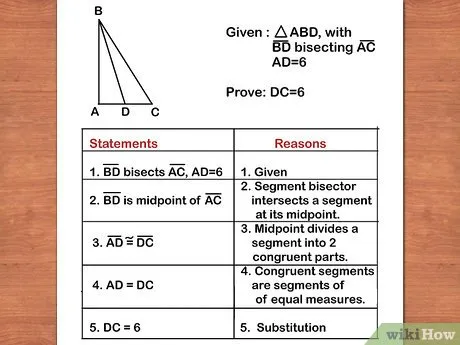
Составьте таблицу в два столбца: в одну колонку запишите утверждения, а в другую — их обоснования. Чтобы достичь строгого доказательства, необходимо пройти через ряд промежуточных предположений и доказать их истинность. Внизу, под колонками с предположениями, необходимо записать конечное утверждение, например, угол ABC равен углу DEF. В колонке обоснований укажите доказательства соответствующих утверждений и предположений. Если утверждение дано в условии задачи, просто напишите в соответствующей ячейке «дано», а если нет — предоставьте доказательство этого утверждения (например, укажите использованную теорему).

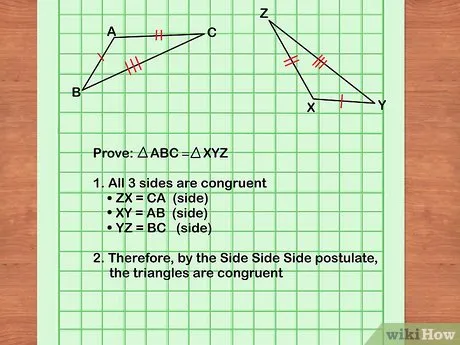
• Согласно теореме, соответствующие стороны конгруэнтных треугольников равны друг другу;
• Если три стороны одного треугольника равны трём сторонам другого треугольника, тогда эти треугольники будут конгруэнтны;
• Если два треугольника имеют две равные стороны и угол между ними, тогда такие треугольники конгруэнтны;
• Если одна сторона одного треугольника равна стороне второго треугольника, а два прилежащих к ней угла равны соответствующим углам второго треугольника, тогда такие треугольники будут конгруэнтны;
• Треугольники с тремя равными углами подобны, но необязательно конгруэнтны.

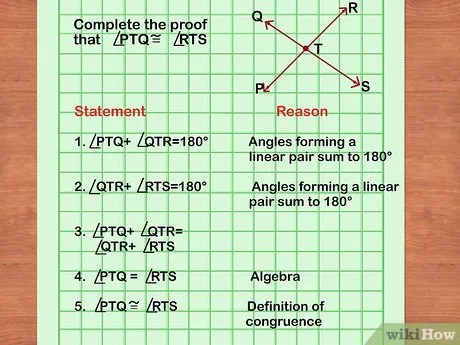
Виды геометрии

Геометрия, как наука, делится на различные подразделы и типы:

• Планиметрия — область геометрии, изучающая свойства фигур и объектов только в рамках одной плоскости. Примеры таких фигур включают треугольники, трапеции, окружности.

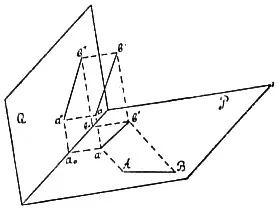
• Стереометрия — область геометрии, в которой исследуются свойства фигур и объектов в трехмерном пространстве. Она включает внимание к углам между плоскостями (двугранные углы), а также к таким фигурам, как сфера, пирамида, призма и другие.
• Аналитическая геометрия — это раздел геометрии, в котором решаются задачи с использованием методов алгебры и координатного анализа. Например, плоские фигуры исследуются с помощью двумерных координат (x; y) для каждой точки. Трехмерные фигуры анализируются с применением (x, y, z). Примером уравнения для прямой на плоскости является уравнение вида y = k * x + b. Используя состояния двух прямых и их уравнения, можно найти точку пересечения этих прямых или проверить их параллельность. Координаты вершин треугольника позволяют найти стороны, а затем вычислить площадь с помощью формулы Герона S = p(p — a)(p — b)(p — c), где p — это полупериметр треугольника. В аналитической геометрии могут использоваться признаки параллельности и перпендикулярности между прямыми и плоскостями.
• Начертательная геометрия — это вид геометрии, изучающий пространственные фигуры через их проекции на плоскостях. Обычно эта геометрия изучается на инженерных специальностях в высших учебных заведениях.
• Дифференциальная геометрия — это раздел высшей математики, на котором свойства фигур исследуются с помощью интегрального и дифференциального исчисления, а также инструментов линейной алгебры и дифференциальных уравнений. Основоположником этой геометрии считается русский математик Н.И. Лобачевский (1792—1856). Данный раздел также называется неевклидовой геометрией, так как аксиома о том, что через точку вне прямой на данной плоскости существует лишь одна прямая, которая ей параллельна, здесь не верна.

Литература

• Бекаревич А. Н. Уравнения в школьном курсе математики. — Минск: Нар. асвета, 1968. — 152 с.
• Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
  • Переиздание: Изд. АСТ, 2003, ISBN 5-17-009554-6.
  1. ↑Глав. ред. М.Д. Аксенова. Энциклопедия для детей. Том 11. Математика. — Изд. 1-е. — М.: Аванта+, 1999. — 688 с. — ISBN 5-89501-018-0.
  2. ↑Филиппов А. Ф. Введение в теорию дифференциальных уравнений. — Изд. 2-е. — 2007. — 240 с. — ISBN 5354004160.
  3. ↑Якушева Е.В., Попов А.В., Якушев А.Г. Математика. Всё для экзамена. — М.: УНЦ ДО, 2004. — 207 с. — ISBN 5-88800-226-7.
  4. ↑Мищенко А.С., Фоменко А.Т. Курс дифференциальной геометрии и топологии. — М.: Факториал Пресс, 2000. — 448 с. — ISBN 5-88688-048-8.

  Данная статья считается завершенной. Это не гарантирует ее высокое качество, но в ней достаточно раскрыты основные темы. Если у вас есть желание улучшить статью, вы можете вносить изменения на свое усмотрение!